Resumen de How not to be wrong de Jordan Ellenberg

Las matemáticas como una extensión del sentido común. Jordan Ellenberg, el autor de How Not to Be Wrong: The Power of Mathematical Thinking ha escrito un libro sobre matemáticas, pero principalmente se trata de como las matemáticas juegan un papel crucial en nuestro día a día sin que nos demos cuenta. Este es el resumen del libro.

Pero, de verdad voy a usar esto alguna vez en mi vida ? Me pregunta mi hijo mayor. Podríamos contestar argumentando que es posible en función de los estudios que elija en el futuro se puede aprovechar este conocimiento, sin embargo nosotros sabríamos que es mentira. Afortunadamente hay una respuesta mejor, al hacer integrales o ecuaciones estás desarrollando una habilidad, no por el simple hecho de resolver la integral en si misma, sino por el propio razonamiento llevado a cabo. Es similar a cuando un jugador de futbol hace burpees, es improbable que en medio de un partido necesite esta habilidad, sin embargo la fuerza obtenida durante dicha práctica si que la podrá aprovechar. Así de emocionante comienza el libro.

Resumen del libro

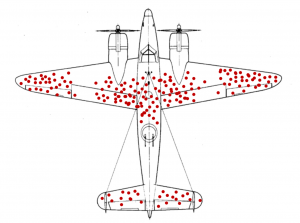
Los puntos rojos a lo largo del avión señalan los agujeros de bala con los que regresaban los aviones a la base

Uno de los primeros ejemplos del libro es el sesgo del superviviente, expuesto por el matemático Abraham Wald durante la segunda guerra mundial. Al regresar los aviones a la base, el fuselaje estaba lleno de agujeros de bala, entonces se plantearon reforzar el avión en aquellos lugares en los que había mayor concentración de agujeros. Sin embargo, cuando le preguntaron a Wald su respuesta fué que el refuerzo se debía hacer justo donde NO había agujeros de bala, pues los aviones que sufrían balas en esos sitios simplemente no regresaban. Dicho razonamiento dejó a los ingenieros con la boca abierta y este sesgo es ampliamente aplicado hoy en día. Los fondos de acciones en una categoría determinada en Morningstar han marcado un crecimiento de un 10.8% anual desde 1995 hasta 2004, lo que suena genial si tuviéramos dinero para invertir. Sin embargo en este tipo de estudios no se tiene en cuenta aquellos fondos que han dejado de existir. Es por ello que judgar los fondos unicamente por aquellos que han sobrevivido es exactamente igual que judgar las habilidades del piloto que ha regresado con vida.

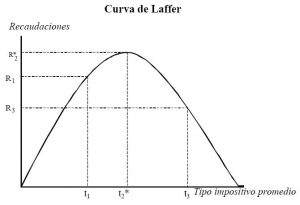
La curva de Laffer tal y como se dice que la escribió en la servilleta

Otro interesante pasaje del libro nos habla sobre la curva de Laffer, se trata de una campana en el que el eje horizontal indica el porcentaje de impuestos a recaudar a los ciudadanos (desde 0 hasta 100) y en el eje vertical los ingresos recibidos por el gobierno. Lo ideal es encontrar el punto intermedio, pues si los ciudadanos pagan pocos impuestos el gobierno no podrá realizar sus funciones, si por el contrario los ciudadanos pagan muchos impuestos, los ingresos también bajarán porque muchas personas trataran de evadir los mismos. Lo interesante de la representación es que la leyenda que la rodea. Corría el año 1974 y Arthur Laffer dibujó la curva en una servilleta para tratar de explicarle a Dick Cheney y a Donald Rumsfeld que si bajaban los impuestos podrían aumentar la recaudación fiscal. La sencillez de la idea llevó al economista Hal Varian a decir que «Se lo puedes explicar a un congresista en 6 minutos y él puede estar hablando de la idea durante 6 horas».

Que pasaría si recibiésemos 10 emails con predicciones que se hicieran realidad, creeríamos al que nos las ha enviado ?

Reflexiona sobre esto por un momento: Un día recibes un email de un broker (que llamaremos el Broker de Baltimore) que sabe que las acciones de una compañía determinada van a dispararse. Pasa una semana y tal y como predijo el broker, las acciones de dicha compañía han subido. A la semana siguiente recibes otro email del mismo broker asegurándote que conoce otra compañía cuyas acciones esta vez se van a desplomar. Efectivamente a la semana siguiente compruebas que estaba en lo cierto. Al décimo correo que recibes del broker, éste te pide que inviertas dinero (con una comisión estupenda, por supuesto) con él. Como para pensárselo, verdad … avaricioso ? El caso es que desde la perspectiva del broker, enviando la suficiente cantidad de emails cuyas probabilidades de acierto son siempre del 50% (consideramos un éxito acertar en la predicción y un fracaso no acertar) al cabo de 9 ó 10 emails habrá convencido a una buena cantidad de personas de que es un excelente broker y se habrá ganado la confianza de unos cuantos. Por poner un ejemplo, supongamos que enviamos 10.240 emails (la mitad dicen que las acciones suben y la otra mitad dicen lo contrario), en caso que las acciones hayan subido, el siguiente mailing unicamente se enviará a los que hayamos acertado (5.120) con mensajes  contrapuestos nuevamente. Al cabo de otra semana tendremos a 2.560 personas convencidas de que somos unos cracks. Una bonita parábola que no está demostrado que se haya puesto.

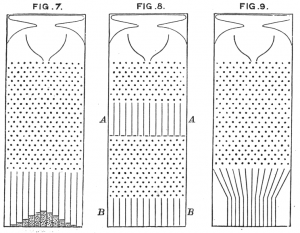
La máquina de Francis Galton y la distribución normal

Los hijos de padres exageradamente altos es probable que sean altos … o no ? Es habitual que si eres un tipo muy alto y tienes un hijo, la gente espera que éste sea alto, más incluso que tú. Sin embargo la conclusión del estadista y genetista Francis Galton no fué esa. Según su estudio de finales del siglo XIX con la publicación de Regression towards mediocrity in hereditary stature si un parámetro como la estatura se dispara con respecto a la media, la herencia de dicho individuo tenderá a regresar a la media, aunque probablemente sea mas alto que la media, no lo será tanto como su progenitor. Es lo que se conoce como Regresión a la media y es más común de lo que nos podríamos pensar. Aquí podemos ver la caja de Galton ( llamada quincux por su agrupación similar al número 5 de un dado) que visualiza la distribución normal, donde no podemos predecir donde va a caer cada una de los bolitas, sin embargo si podemos estimar como se comportará el conjunto de ellas.

Estos son solo algunos ejemplos de la gran cantidad de temas interesantes que repasa Jordan Ellenberg en The Power Of Mathematical Thinking.

Temas tan interesantes como la falacia de Berkson, la correlación, la geometría proyectiva o la reducción al absurdo son solo algunos ejemplos de lo que nos podemos encontrar en el interior del libro.

Porqué Leerlo ?

The Power Of Mathematical Thinking de Jordan Ellenberg es un libro que habla de las matemáticas desde un punto de vista al que no estamos acostumbrados, y se centra en como éstas influyen en la vida real sin que nos demos cuenta. Además es uno de los libros recomendados por Bill Gates en 2018.

Te ha gustado este resumen ? En mi página de libros puedes ver todos los resúmenes que voy haciendo.